|
dft-overview
|
|
dft-tex,
dft.html,
dft_biol.html,
dft_dft.html,
dft_fof.html,
dft_hamil.html,
dft_hk.html,
dft_intro.html,
dft_perf.html,
dft_refs.html,
dft_scfks.html,
dft_wave.html,
foot_motif.gif,
footnode.html,
image.gif,
img1.gif,
img10.gif,
img100.gif,
img101.gif,
img102.gif,
img103.gif,
img104.gif,
img105.gif,
img106.gif,
img107.gif,
img108.gif,
img109.gif,
img11.gif,
img110.gif,
img111.gif,
img112.gif,
img113.gif,
img114.gif,
img115.gif,
img116.gif,
img117.gif,
img118.gif,
img119.gif,
img12.gif,
img120.gif,
img121.gif,
img122.gif,
img123.gif,
img124.gif,
img125.gif,
img126.gif,
img127.gif,
img128.gif,
img129.gif,
img13.gif,
img130.gif,
img131.gif,
img132.gif,
img133.gif,
img134.gif,
img135.gif,
img136.gif,
img137.gif,
img138.gif,
img139.gif,
img14.gif,
img140.gif,
img141.gif,
img142.gif,
img143.gif,
img144.gif,
img145.gif,
img146.gif,
img147.gif,
img148.gif,
img149.gif,
img15.gif,
img150.gif,
img151.gif,
img152.gif,
img153.gif,
img154.gif,
img155.gif,
img156.gif,
img157.gif,
img158.gif,
img159.gif,
img16.gif,
img160.gif,
img161.gif,
img162.gif,
img163.gif,
img164.gif,
img165.gif,
img166.gif,
img167.gif,
img168.gif,
img169.gif,
img17.gif,
img170.gif,
img171.gif,
img172.gif,
img173.gif,
img174.gif,
img175.gif,
img176.gif,
img177.gif,
img178.gif,
img179.gif,
img18.gif,
img180.gif,
img181.gif,
img182.gif,
img183.gif,
img184.gif,
img185.gif,
img186.gif,
img187.gif,
img188.gif,
img189.gif,
img19.gif,
img190.gif,
img191.gif,
img192.gif,
img193.gif,
img194.gif,
img195.gif,
img196.gif,
img197.gif,
img198.gif,
img199.gif,
img2.gif,
img20.gif,
img200.gif,
img201.gif,
img202.gif,
img203.gif,
img204.gif,
img205.gif,
img206.gif,
img207.gif,
img208.gif,
img209.gif,
img21.gif,
img210.gif,
img211.gif,
img212.gif,
img213.gif,
img214.gif,
img215.gif,
img216.gif,
img217.gif,
img218.gif,
img219.gif,
img22.gif,
img220.gif,
img221.gif,
img222.gif,
img223.gif,
img224.gif,
img225.gif,
img226.gif,
img227.gif,
img228.gif,
img229.gif,
img23.gif,
img230.gif,
img231.gif,
img232.gif,
img233.gif,
img234.gif,
img235.gif,
img236.gif,
img237.gif,
img238.gif,
img239.gif,
img24.gif,
img240.gif,
img241.gif,
img242.gif,
img243.gif,
img244.gif,
img245.gif,
img246.gif,
img247.gif,
img248.gif,
img249.gif,
img25.gif,
img250.gif,
img251.gif,
img252.gif,
img253.gif,
img254.gif,
img255.gif,
img256.gif,
img26.gif,
img27.gif,
img28.gif,
img29.gif,
img3.gif,
img30.gif,
img31.gif,
img32.gif,
img33.gif,
img34.gif,
img35.gif,
img36.gif,
img37.gif,
img38.gif,
img39.gif,
img4.gif,
img40.gif,
img41.gif,
img42.gif,
img43.gif,
img44.gif,
img45.gif,
img46.gif,
img47.gif,
img48.gif,
img49.gif,
img5.gif,
img50.gif,
img51.gif,
img52.gif,
img53.gif,
img54.gif,
img55.gif,
img56.gif,
img57.gif,
img58.gif,
img59.gif,
img6.gif,
img60.gif,
img61.gif,
img62.gif,
img63.gif,
img64.gif,
img65.gif,
img66.gif,
img67.gif,
img68.gif,
img69.gif,
img7.gif,
img70.gif,
img71.gif,
img72.gif,
img73.gif,
img74.gif,
img75.gif,
img76.gif,
img77.gif,
img78.gif,
img79.gif,
img8.gif,
img80.gif,
img81.gif,
img82.gif,
img83.gif,
img84.gif,
img85.gif,
img86.gif,
img87.gif,
img88.gif,
img89.gif,
img9.gif,
img90.gif,
img91.gif,
img92.gif,
img93.gif,
img94.gif,
img95.gif,
img96.gif,
img97.gif,
img98.gif,
img99.gif
|
|
|
Molecular DFT
Introduction to Molecular Approaches of Density Functional Theory
Ohio Supercomputer Center, 1224 Kinnear Rd, Columbus, OH 43221-1153
Return to index
Typical Program Organization for SCF-KS equations
The single geometry SCF cycle or geometry optimization
involve following steps:
- 1.
- Start with a density (for the 1st iteration, superposition of atomic
densities is typically used).
- 2.
- Establish grid for charge density and exchanger correlation potential
- 3.
- Compute KS matrix (equivalent to the
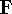 matrix in Hartree-Fock
method in equation (57)) elements and overlap integrals matrix. matrix in Hartree-Fock
method in equation (57)) elements and overlap integrals matrix.
- 4.
- Solve the equations for expansion coefficients to obtain KS orbitals.
- 5.
- Calculate new density
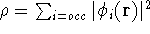 . .
- 6.
- If density or energy changed substantially, go to step 1.
- 7.
- If SCF cycle converged and geometry optimization is not requested, go to step 10.
- 8.
- Calculate derivatives of energy vs. atom coordinates, and update atom
coordinates. This may require denser integration grids and recomputing of
Coulomb and exchange-correlation potential.
- 9.
- If gradients are still large, or positions of nuclei moved appreciably, go to step 1.
- 10.
- Calculate properties and print results.
Of course, there may be other variants of this method (e.g., when one computes
vibrational frequencies from the knowledge of gradients and energies only).
It is quite popular to limit expense of numerical integration during the SCF cycle.
It is frequently done by fitting auxiliary functions to charge density and exchange
correlation potential. This allows for much faster integral evaluation.
These auxiliary fitting functions are usually uncontracted gaussians (though quite different
from the atomic basis sets) for which the integrals required for KS matrix can be
calculated analytically. Different auxilliary sets are used for fitting charge density
and exchange-correlation potential (see e.g., Dunlap & Rösch, 1990). The need for
fitting is recently questioned (see e.g., Johnson, 1995) since it scales
as 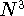 even for very large systems, however, it is still very popular in
DFT codes. The fitting procedures are in general non sparse, while for large
molecules many contributions coming from distant portions may be neglected
leading to less steep scaling with molecular size. even for very large systems, however, it is still very popular in
DFT codes. The fitting procedures are in general non sparse, while for large
molecules many contributions coming from distant portions may be neglected
leading to less steep scaling with molecular size.
Early DFT codes were impaired by the lack of analytical gradients.
Currently, expressions for first and second derivatives exist
(see e.g.: Dunlap & Andzelm, Komornicki & Fitzgerald, 1993)
and are implemented in many programs, thus facilitating geometry
optimization and vibrational frequency calculations.
Return to index
Next Section
|
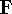 matrix in Hartree-Fock
method in equation (57)) elements and overlap integrals matrix.
matrix in Hartree-Fock
method in equation (57)) elements and overlap integrals matrix.
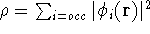 .
.
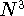 even for very large systems, however, it is still very popular in
DFT codes. The fitting procedures are in general non sparse, while for large
molecules many contributions coming from distant portions may be neglected
leading to less steep scaling with molecular size.
even for very large systems, however, it is still very popular in
DFT codes. The fitting procedures are in general non sparse, while for large
molecules many contributions coming from distant portions may be neglected
leading to less steep scaling with molecular size.
