Ohio Supercomputer Center, 1224 Kinnear Rd, Columbus, OH 43221-1153
 (e.g., some
approximate one) for a system and calculate the expectation value
of energy E, this energy will be either higher, or equal to the
ground state energy
(e.g., some
approximate one) for a system and calculate the expectation value
of energy E, this energy will be either higher, or equal to the
ground state energy 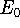 for this system.
for this system.
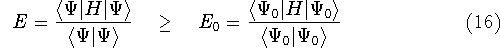
The 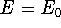 occurs only if
occurs only if  is equivalent to
is equivalent to 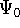 , but otherwise,
, but otherwise,
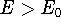 . This theorem can be easily proven (see for example: Levine, 1983; Slater, 1968, or
Szabo & Ostlund, 1989).
What is more important however, that this theorem provides us with the prescription
how to find the good wave function: try to go as low with the expectation value of
energy, as you can (you cannot go lower than the true value). And the lower you go,
the better you are. The word of caution here... The principle is true only
if we are applying a true hamiltonian in the expression for expectation energy.
Of course, if your hamiltonian does not represent a physical system, you can
get whatever you wish,
. This theorem can be easily proven (see for example: Levine, 1983; Slater, 1968, or
Szabo & Ostlund, 1989).
What is more important however, that this theorem provides us with the prescription
how to find the good wave function: try to go as low with the expectation value of
energy, as you can (you cannot go lower than the true value). And the lower you go,
the better you are. The word of caution here... The principle is true only
if we are applying a true hamiltonian in the expression for expectation energy.
Of course, if your hamiltonian does not represent a physical system, you can
get whatever you wish,  included!!!
included!!!
As said before, we can rarely solve the Schrödinger equation exactly. And we have to use approximations.
The first successful attempt to derive approximate wave functions
for atoms was devised by Hartree (1928).
In this approach the many-electron wave function  is approximated
by the product of one-electron functions
is approximated
by the product of one-electron functions 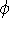 for each of the N electrons:
for each of the N electrons:
In this equation,  are the positional coordinates and a spin coordinate
for the i-th electron. For example, in cartesians
are the positional coordinates and a spin coordinate
for the i-th electron. For example, in cartesians 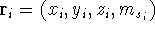 ,
though to solve this equation for atoms, the spherical coordinates are more
useful
,
though to solve this equation for atoms, the spherical coordinates are more
useful  ,
where
,
where 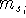 can adopt only 2 values:
can adopt only 2 values:  /
/ 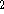 (spin up,
or
(spin up,
or  or
or 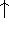 ) or
) or 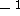 /
/ 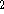 (spin down,
(spin down, 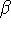 , or
, or
 ). The individual one-electron functions
). The individual one-electron functions  are called orbitals,
(or spinorbitals) and describe each electron in the atom (or molecule).
Is this a reasonable approximation? Not really...
are called orbitals,
(or spinorbitals) and describe each electron in the atom (or molecule).
Is this a reasonable approximation? Not really...
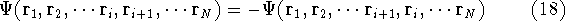
e.g., 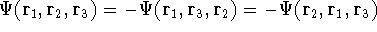 .
.
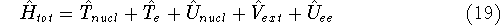
where
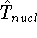 is the operator of kinetic energy of nuclei,
is the operator of kinetic energy of nuclei,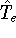 represents the kinetic energy of electrons,
represents the kinetic energy of electrons,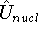 is the interaction energy of nuclei (Coulombic repulsion),
is the interaction energy of nuclei (Coulombic repulsion),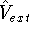 is the external potential (in this case, the
electrostatic potential coming form nuclei, with which electrons interact),
is the external potential (in this case, the
electrostatic potential coming form nuclei, with which electrons interact),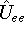 denotes electrostatic repulsion between electrons.
denotes electrostatic repulsion between electrons.
Since nuclei are much heavier than electrons (a proton is
1836 times heavier than an electron),
they have much larger intertia than electrons, and we can consider that electrons will adjust
their positions instantly whenever nuclei move. Prof. Rod Bartlett once used an analogy of
flies around the wedding cakes - you move the cakes, and the flies move with them.
Without much error, we can therefore separate the movement of electrons and nuclei, and
assume that the movement of electrons depends on positions of nuclei in a parametric way.
This is the contents of the Born-Oppenheimer (1927) approximation. It allows us to use the electronic
hamiltonian  to study electrons, and add the components of energy coming from nuclei
(i.e., their kinetic energy,
to study electrons, and add the components of energy coming from nuclei
(i.e., their kinetic energy, 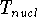 , and internuclear repulsion energy,
, and internuclear repulsion energy, 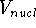 ) at the
end of calculations.
) at the
end of calculations.
The form of these operators will be given below. Atomic units are used here,
i.e., mass of electron 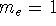 ;
;
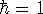 ; length is expressed in bohrs (1 bohr = 0.529177249Å; it is the
radius of the first Bohr orbit in hydrogen atom);
energy is in hartrees (1 hartree is 2 rydbergs, and the ground state energy
of hydrogen atom is -1 rydberg, or 0.5 hartree, 1 hartree = 627.51 kcal/mol = 2625.5 kJ/mol);
1 unit of charge is a charge of a proton, the gaussian electrostatic system is used (the unit
of permittivity is
; length is expressed in bohrs (1 bohr = 0.529177249Å; it is the
radius of the first Bohr orbit in hydrogen atom);
energy is in hartrees (1 hartree is 2 rydbergs, and the ground state energy
of hydrogen atom is -1 rydberg, or 0.5 hartree, 1 hartree = 627.51 kcal/mol = 2625.5 kJ/mol);
1 unit of charge is a charge of a proton, the gaussian electrostatic system is used (the unit
of permittivity is 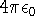 and it does not appear in the Coulomb law for vacuum).
and it does not appear in the Coulomb law for vacuum).
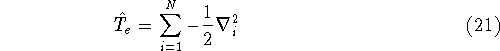
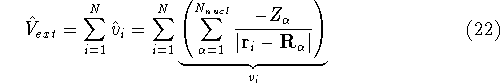
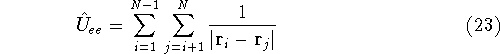
Here, the  is the charge of an
is the charge of an  -th nucleus
(atomic number),
-th nucleus
(atomic number), 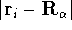 is the distance between electron i and the nucleus
is the distance between electron i and the nucleus
 ,
, 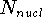 is the total number of nuclei in the molecule
(but it is obviously equal to 1 for an atom),
is the total number of nuclei in the molecule
(but it is obviously equal to 1 for an atom), 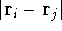 is the distance between
electron i and j. Note, that
is the distance between
electron i and j. Note, that 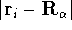 and
and 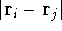 can be expressed in cartesian coordinates:
can be expressed in cartesian coordinates:
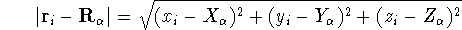
(note that nuclear coordinates for each of the 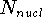 nuclei:
nuclei:
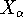 ,
, 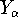 ,
,  are constants/parameters rather
than variables in the electronic hamiltonian
are constants/parameters rather
than variables in the electronic hamiltonian  ),
),
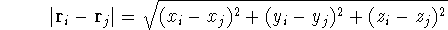
We can rewrite again the electronic hamiltionian:
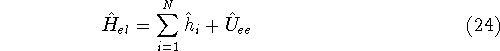
where operator
and 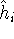 only depends on coordinates of
only depends on coordinates of  of
a given i-th electron. In the product function from equation (17),
of
a given i-th electron. In the product function from equation (17), 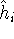 would only affect the
function for the i-th electron. Unfortunately, there is still this
would only affect the
function for the i-th electron. Unfortunately, there is still this 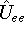 which depends on
pairs of electrons, and we cannot separate variables in the the Schrödinger equation,
(a second order differential equation). So, Hartree found an approximation, in which
electron does not interact with other electrons one by one,
but with the averaged density of electrons. If we assume for the moment
that we know the one-electron functions
which depends on
pairs of electrons, and we cannot separate variables in the the Schrödinger equation,
(a second order differential equation). So, Hartree found an approximation, in which
electron does not interact with other electrons one by one,
but with the averaged density of electrons. If we assume for the moment
that we know the one-electron functions 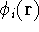 , for each electron
(they make the total wave function in equation (17))
we can calculate densities corresponding to each electron
using equation (12):
, for each electron
(they make the total wave function in equation (17))
we can calculate densities corresponding to each electron
using equation (12):

And the total density of the electrons will be a sum of individual electron densities:
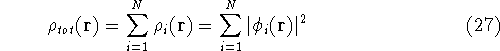
However, the k-th electron does not interact with the whole density  , since
it is itself a part of it. Electron cannot interact with itself!
It is not a human being!!! This would be a self-interaction. So, if we want to
find a correct density with which the k-th electron interacts (let us denote
it by
, since
it is itself a part of it. Electron cannot interact with itself!
It is not a human being!!! This would be a self-interaction. So, if we want to
find a correct density with which the k-th electron interacts (let us denote
it by 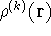 ), we need to subtract its own
density from
), we need to subtract its own
density from  :
:
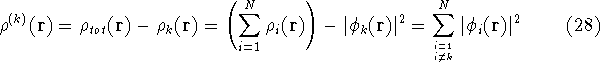
Now, let us assume that we know some approximate functions for the orbitals.
And we want to calculate the energy of interation of point charge (our electron)
located at position  , with other electrons represented as a smeared electron density.
Out point charge is -e, which in atomic units is -1, and the electron density is also negative,
so we get a positive contribution to energy:
, with other electrons represented as a smeared electron density.
Out point charge is -e, which in atomic units is -1, and the electron density is also negative,
so we get a positive contribution to energy:
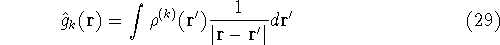
Now, if we make such an approximation, we can write:
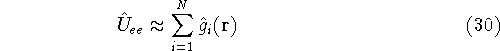
(it is not entirely true, as we will see later, since we doubly count
interaction, but let us leave it at that for a moment),
and our  consists of sums of one-electron operators:
consists of sums of one-electron operators:

and the many electron Schrödinger equation can be solved as N independent one electron equations:
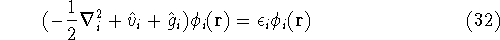
The 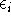 is the energy of the i-th electron.
In practice, we start with some approximate orbitals
is the energy of the i-th electron.
In practice, we start with some approximate orbitals  (e.g., from
hydrogen atom). We need them, since the
(e.g., from
hydrogen atom). We need them, since the 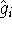 depends on them.
We solve all N equations and obtain the N new
depends on them.
We solve all N equations and obtain the N new 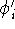 's.
The new
's.
The new 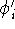 's are different from the old
's are different from the old  's, and we believe
that they are better. And now we have
better approximations for orbitals, and use the new
's, and we believe
that they are better. And now we have
better approximations for orbitals, and use the new  's as a starting point
and repeat the process. At some point,
's as a starting point
and repeat the process. At some point,  's do not change from iteration
to iteration, and we obtained the self-consistent field orbitals.
From these orbitals we can form a many electron wave function
's do not change from iteration
to iteration, and we obtained the self-consistent field orbitals.
From these orbitals we can form a many electron wave function  ,
and then calculate the total energy E of the ground state.
Note, that the total energy is not equal to the sum of orbital energies
,
and then calculate the total energy E of the ground state.
Note, that the total energy is not equal to the sum of orbital energies 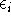 .
We calculate the expectation value of energy using the accurate hamiltonian
.
We calculate the expectation value of energy using the accurate hamiltonian
 from equation (20).
When we solved equation for
from equation (20).
When we solved equation for 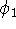 and
and  we included the
Coulomb interactions between electron: (1, 2), (1, 3), (1, 4), etc.
When we solved second equation, we included interactions:
(2, 1), (2, 3), (2, 4), etc. But the interaction (1, 2) is the same
as (2, 1), i.e., adding the energies we would count interactions twice.
For this reason, the correct total energy can be represented as:
we included the
Coulomb interactions between electron: (1, 2), (1, 3), (1, 4), etc.
When we solved second equation, we included interactions:
(2, 1), (2, 3), (2, 4), etc. But the interaction (1, 2) is the same
as (2, 1), i.e., adding the energies we would count interactions twice.
For this reason, the correct total energy can be represented as:
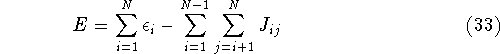
where 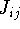 's represent Coulomb interaction of electron i and j. They are
called Coulomb integrals and are defined as:
's represent Coulomb interaction of electron i and j. They are
called Coulomb integrals and are defined as:
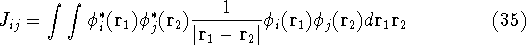
The Hartree approximation works well for atoms. The one-electron functions are quite good, and allow us to produce an approximate many-electron function for the whole atom. But the form of the function adopted by Hartree was basically wrong. It was known at that time that interchanging the electron labels in the wave functions for the system of electrons has to change its sign. This is not something which can be derived. It is simply a law of nature. And it is important, since without this property, the function will not correctly describe the system. Electrons (fermions) have this propery, and we should use it. In the system of fermions, no two particles can be described by the same one particle function. So, few years later, Fock (1930), and independently Slater(1930) proposed a fix to the Hartree method. They also used one-electron functions, but the total wave function for the system was not a simple product of orbitals, but an antisymmetrized sum of all the products which can be obtained by interchanging electron labels. It is conveniently represented as a determinant (called Slater determinant):
Let us examine some properties of this function taking a 2-electron case:
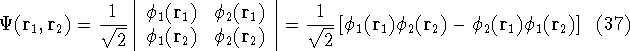
If we change electron labels  and
and  we get
we get
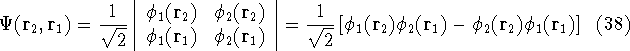
that is: 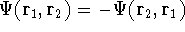 .
Moreover, if we assume that two electrons are described by the same spinorbital:
.
Moreover, if we assume that two electrons are described by the same spinorbital:
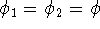 we get:
we get:
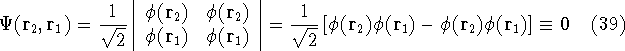
i.e., such wave function whould be zero everywhere, and hence, the probablility of finding
such electrons is zero. So, Slater determinant satisfies the Pauli exclusion
principle that each electron has to be described by a different wave function.
It was originally formulated by Pauli (1925) for electrons in atoms, that no two
electrons can have the same values of all four quantum numbers: n, l, 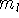 , and
, and 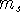 .
The single determinant wave function is much better than the Hartree product
function as it naturally includes some basic fermion characteristics.
.
The single determinant wave function is much better than the Hartree product
function as it naturally includes some basic fermion characteristics.
However, it complicates equations compared to Hartree method and introduces a new term, electron exchange. The method of finding the best single determinant wave function for the system is called Hartree-Fock method.
The expectation value of total energy for the single determinant wave function  is given by:
is given by:

where:
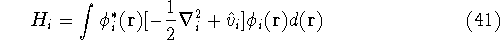
is an element of one-electron operator 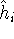 which was defined by equation (25),
the
which was defined by equation (25),
the 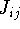 is the Coulomb integral defined by equation
(34), and
is the Coulomb integral defined by equation
(34), and  is the new
term, called exchange integral, which is defined by
is the new
term, called exchange integral, which is defined by
Note, that  is similar in form to the
is similar in form to the 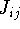 but the functions
but the functions  and
and 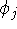 were exchanged. Also, electrons i and j have to be of the same spin for
were exchanged. Also, electrons i and j have to be of the same spin for  to be
nonzero, due to othogonality of their spin parts. It does not have a simple physical
interpretation like
to be
nonzero, due to othogonality of their spin parts. It does not have a simple physical
interpretation like 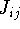 (i.e., purely electrostatic interaction
of two charge densities for electron i and j).
The exchange integral comes as a result of the determinantal form of
(i.e., purely electrostatic interaction
of two charge densities for electron i and j).
The exchange integral comes as a result of the determinantal form of  which
sums all possible products of permutations of electrons among orbitals.
which
sums all possible products of permutations of electrons among orbitals.
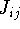 and
and  are equal only when i=j. This is very
important, since there is
no contribution to the total energy coming from electron self-interaction.
It can be shown that
are equal only when i=j. This is very
important, since there is
no contribution to the total energy coming from electron self-interaction.
It can be shown that 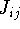 's are larger (or equal to)
's are larger (or equal to)  's and they are positive numbers.
's and they are positive numbers.
There are essentially two approaches to HF method: purely numerical,
and the one in which orbitals 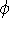 are represented as combinations
of basis functions. The numerical HF was used at some
point to derive orbitals for many-electron atoms. There are also some
numerical HF programs for molecules. However, these methods are
quite intensive. It is much more popular to represents orbitals
are represented as combinations
of basis functions. The numerical HF was used at some
point to derive orbitals for many-electron atoms. There are also some
numerical HF programs for molecules. However, these methods are
quite intensive. It is much more popular to represents orbitals 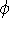 as a linear expansion into a set of some basis functions
as a linear expansion into a set of some basis functions 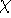 :
:
and optimizing coefficients 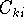 rather than basis functions.
rather than basis functions.
The derivation of specific equations for Hartree-Fock
method will not be given
here, but can be found in many books, (see, e.g.:
McWeeny & Sutcliffe, 1969; Parr, 1963; Pilar, 1968;
Slater, 1968; Szabo & Ostlung, 1989) and landmark papers
of Roothaan (1951, 1960).
In the SFC LCAO MO (Self Consistent Field - Linear
Combination of Atomic Orbitals, Molecular Orbitals) method,
we are looking for the coefficients 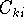 which minimize the energy.
which minimize the energy.
They are derived using varational principle, i.e.
the goal here is to find a single determinant function  as represented by
equation (36) which corresponds to the lowest possible value of energy.
It is done by the variational calculus. The condition of minimum of energy is:
as represented by
equation (36) which corresponds to the lowest possible value of energy.
It is done by the variational calculus. The condition of minimum of energy is:

Another condition is that orbitals 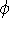 have to be
orthonormal, i.e.:
have to be
orthonormal, i.e.:

where 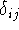 is called a Kronecker delta, and is equal to
1 only if i=j, but is zero otherwise.
is called a Kronecker delta, and is equal to
1 only if i=j, but is zero otherwise.
The problem of minimization of a function with some subsidiary conditions is done efficiently with the Lagrange's method of undetermined multipliers. In this method, the constraints are converted into expressions whose value is zero when the constraint is met. Such expressions are then multiplied by an undetermined constant and added (or subtracted, according to taste) to the minimized function. The resulting sum is then minimized:
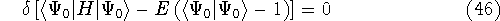
As a result, one gets Hartree-Fock eigenequations.
where the Fock operator is defined as:
In these equations, the fact that operators act on certain coordinates is stressed by writing explicitly
their dependence on coordinates of electron 1 (it could be any electron number, since it does not matter
how we number them). The 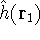 was defined in equation
(25). The Coulomb
operator,
was defined in equation
(25). The Coulomb
operator,
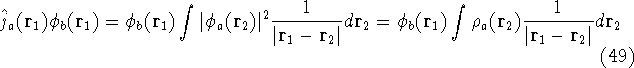
and the exchange operator
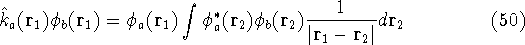
are defined by the result of their action on a function.
If we now introduce basis, i.e., replace  's with their expansions into basis functions
according to equation (43), the eigenproblems become a set of algebraic equations.
Substituting equation (43) into (47) one gets:
's with their expansions into basis functions
according to equation (43), the eigenproblems become a set of algebraic equations.
Substituting equation (43) into (47) one gets:
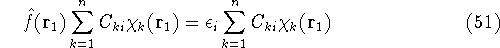
and multiplying on the left by  and integrating over
and integrating over  one gets:
one gets:
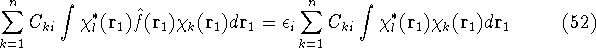
Integrals are further denoted as:
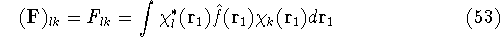
which is an element of a  Fock matrix
Fock matrix 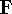 , and
, and
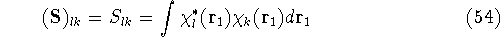
which is an element of a 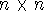 overlap integrals matrix
overlap integrals matrix 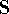 .
We can obtain n (i.e., number of basis functions) of such equations, and it is convenient to
write them in a matrix form as:
.
We can obtain n (i.e., number of basis functions) of such equations, and it is convenient to
write them in a matrix form as:
The problem now is to find such marix  which diagonalizes
which diagonalizes 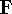 , which is a standard
procedure in linear algebra. First step is to find a matrix
, which is a standard
procedure in linear algebra. First step is to find a matrix 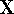 which diagonalizes overlap integrals
which diagonalizes overlap integrals 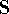 , which is a step ortogonalizing the basis set
(i.e., the basis set is converted to linear combinations of original basis functions, which
are mutually orthogonal).
, which is a step ortogonalizing the basis set
(i.e., the basis set is converted to linear combinations of original basis functions, which
are mutually orthogonal).

Applying this matrix to equation (55) and rearranging it we get
where 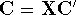 and
and 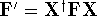 . The efficient routines for
matrix diagonalization (i.e., obtaining
. The efficient routines for
matrix diagonalization (i.e., obtaining 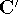 in this case) are widely available.
in this case) are widely available.
While they seem simple, the problem is that elements of 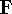 depend on orbitals
depend on orbitals 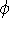 , i.e.,
one can solve them only through iterative process as in Hartree's method. Moreover, due to Coulomb
and exchange operators, the Fock matrix elements involve a massive number of two-electron integrals of a type:
, i.e.,
one can solve them only through iterative process as in Hartree's method. Moreover, due to Coulomb
and exchange operators, the Fock matrix elements involve a massive number of two-electron integrals of a type:

To escape these difficulties and complexities, people tried for many years to
decribe electron systems using density, rather than wave function.
In the HF approach the two-electron integrals 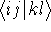 dominate the computational effort.
Moreover, the HF is an approximation, as it does not account for dynamic correlation
due to the rigid form of single determinant wave function. To solve the HF equations,
the assumption has to be made that electrons interact with the averaged potential coming
from other electrons, while in fact, the interactions between electrons are pairwise.
In reality, electrons correlate their movements trying to avoid each other, so there is least
amount of electrostatic repulsion.
To account for dynamic correlation, one has to go to correlated methods, which use multideterminant
wave functions, and these scale as fifth, or even greater powers with the size of a system.
While HF method is quite successful for geometries, it fails miserably to
describe bond breaking or forming (for review of correlated ab initio methods see: Bartlett & Stanton, 1994).
dominate the computational effort.
Moreover, the HF is an approximation, as it does not account for dynamic correlation
due to the rigid form of single determinant wave function. To solve the HF equations,
the assumption has to be made that electrons interact with the averaged potential coming
from other electrons, while in fact, the interactions between electrons are pairwise.
In reality, electrons correlate their movements trying to avoid each other, so there is least
amount of electrostatic repulsion.
To account for dynamic correlation, one has to go to correlated methods, which use multideterminant
wave functions, and these scale as fifth, or even greater powers with the size of a system.
While HF method is quite successful for geometries, it fails miserably to
describe bond breaking or forming (for review of correlated ab initio methods see: Bartlett & Stanton, 1994).