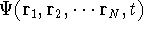 (where the
(where the 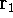 denotes the coordinates of the 1st electron,
denotes the coordinates of the 1st electron,
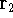 the 2nd electron, and so on, and t is time) and solve the
stationary (time-independent) Schrödinger equation for the system:
the 2nd electron, and so on, and t is time) and solve the
stationary (time-independent) Schrödinger equation for the system:
Ohio Supercomputer Center, 1224 Kinnear Rd, Columbus, OH 43221-1153
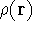 , i.e., the number of electrons per unit volume
at a given point in space (e.g., in cartesian coordinates:
, i.e., the number of electrons per unit volume
at a given point in space (e.g., in cartesian coordinates:
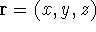 ). In this approach,
electrons were treated as particles forming a special gas, called electron gas.
The special case, the uniform electron gas, corresponds to
the
). In this approach,
electrons were treated as particles forming a special gas, called electron gas.
The special case, the uniform electron gas, corresponds to
the 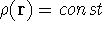 .
.
Another approach was to derive the many particle
wave function 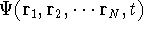 (where the
(where the 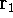 denotes the coordinates of the 1st electron,
denotes the coordinates of the 1st electron,
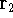 the 2nd electron, and so on, and t is time) and solve the
stationary (time-independent) Schrödinger equation for the system:
the 2nd electron, and so on, and t is time) and solve the
stationary (time-independent) Schrödinger equation for the system:
(where 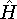 is the hamiltonian, i.e.,
the operator of the total energy for the system),
and calculate the set of possible
wave functions (called eigenfunctions)
is the hamiltonian, i.e.,
the operator of the total energy for the system),
and calculate the set of possible
wave functions (called eigenfunctions) 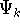 and corresponding
energies (eigenvalues)
and corresponding
energies (eigenvalues) 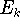 . The eigenfunctions have to be
physically acceptable, and for finite systems:
. The eigenfunctions have to be
physically acceptable, and for finite systems:
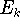 form a complete set of functions, i.e., there is an
infinite number of them, they are orthogonal to each other (or can be
easily made orthogonal through a linear transformation), and
any function which is of ``physical quality'' can be expressed through
the combination of these eigenfunctions. Orthogonal means, that:
form a complete set of functions, i.e., there is an
infinite number of them, they are orthogonal to each other (or can be
easily made orthogonal through a linear transformation), and
any function which is of ``physical quality'' can be expressed through
the combination of these eigenfunctions. Orthogonal means, that:
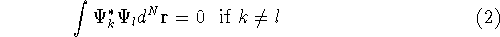
The eigenfunction 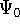 corresponding to the lowest energy
corresponding to the lowest energy 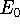 ,
describes the ground state of the system,
and the higher energy values correspond to
excited states. Physicists like to call
,
describes the ground state of the system,
and the higher energy values correspond to
excited states. Physicists like to call  's the states (since they
contain all possible information about the state), while chemists
usually call them wave functions.
's the states (since they
contain all possible information about the state), while chemists
usually call them wave functions.
Once the function
 (or its approximation, i.e., in case
when the Schrödinger equation is
solved only approximately) is known,
the corresponding energy of the system can be calculated
as an expectation value of the hamiltonian
(or its approximation, i.e., in case
when the Schrödinger equation is
solved only approximately) is known,
the corresponding energy of the system can be calculated
as an expectation value of the hamiltonian 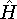 , as:
, as:
where 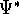 denotes the complex conjugate of
denotes the complex conjugate of  since in general
these functions may produce complex numbers. This is needed since
the operator in this case represents a physical observable, and
the result has to be a real number.
This equation is frequently written using Dirac bra (
since in general
these functions may produce complex numbers. This is needed since
the operator in this case represents a physical observable, and
the result has to be a real number.
This equation is frequently written using Dirac bra ( 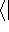 ) and
ket (
) and
ket ( 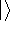 ) notation to save space (and to confuse the innocent):
) notation to save space (and to confuse the innocent):
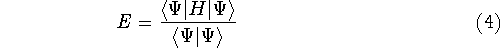
And if 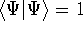 , i.e., the wave function is normalized, the
equation looks even simpler:
, i.e., the wave function is normalized, the
equation looks even simpler:

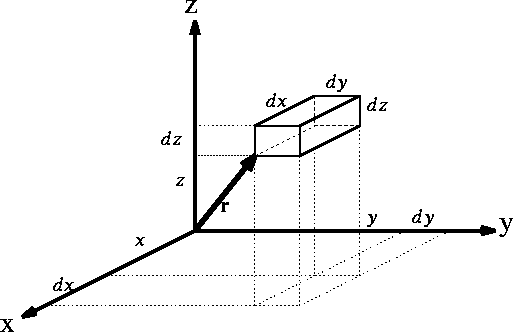
Figure 1: Volume element for a particle
Once we know the wave function  for a given state of our system, we can
calculate the expectation value for any quantity for which we can write down
the operator. The wave function itself does not correspond to any physical quantity,
but its square represents the probablity density. In other words:
for a given state of our system, we can
calculate the expectation value for any quantity for which we can write down
the operator. The wave function itself does not correspond to any physical quantity,
but its square represents the probablity density. In other words:
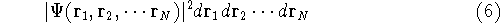
or
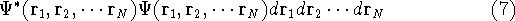
or

represents the probablity that electron 1 is in the volume element 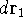 around
point
around
point 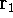 , electron 2 is in the volume element of the size
, electron 2 is in the volume element of the size 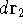 around point
around point 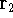 , and so on. If
, and so on. If  describes the system containing only a single
electron, the
describes the system containing only a single
electron, the 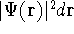 simply represents the probability of finding
an electron in the volume element of a size
simply represents the probability of finding
an electron in the volume element of a size 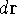 centered around point
centered around point  .
If you use cartesian coordinates, then
.
If you use cartesian coordinates, then 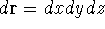 and the volume element would be
a brick (rectangular parallelipiped) with dimensions
and the volume element would be
a brick (rectangular parallelipiped) with dimensions 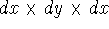 whose
vertex closes to the origine of coordinate system is located at (x, y, z).
Now, if we integrate the function
whose
vertex closes to the origine of coordinate system is located at (x, y, z).
Now, if we integrate the function  over all the space for all the variables (i.e., sum
up the probablilities in all the elements
over all the space for all the variables (i.e., sum
up the probablilities in all the elements 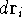 ), we should get a probability
of finding our electrons anywhere in the Universe, i.e., 1. This is why it is a good
idea to normalize fundtion
), we should get a probability
of finding our electrons anywhere in the Universe, i.e., 1. This is why it is a good
idea to normalize fundtion  . If it is not normalized, it can easily be done by
multiplying it by a normalization constant:
. If it is not normalized, it can easily be done by
multiplying it by a normalization constant:

Since square of  represents the probablility density of
finding electrons, one may suspect, that it should be easy to
calculate the total electron density from it. And actually it is:
represents the probablility density of
finding electrons, one may suspect, that it should be easy to
calculate the total electron density from it. And actually it is:
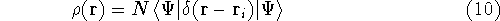
where N is the total number of electrons, and 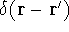 is the famous Dirac delta function. In cartesians, it simply amounts to
integrating over all electron positions vectors
is the famous Dirac delta function. In cartesians, it simply amounts to
integrating over all electron positions vectors  but one.
Which one, is not important, since
electrons are indistinguishable, and a proper wave function has to reflect this:
but one.
Which one, is not important, since
electrons are indistinguishable, and a proper wave function has to reflect this:
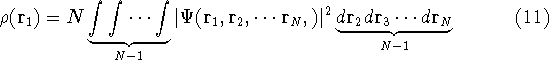
It is interesting to note, that for the wave function which describes the system containing only a single electron (but only then !!!):
i.e., logically, the electron density and the probability density of finding the single electron are the same thing.