Introduction to Molecular Approaches of Density Functional Theory
Ohio Supercomputer Center, 1224 Kinnear Rd, Columbus, OH 43221-1153
Return to index
Performance of DFT
This will be a very short list of DFT applications, as there are many excellent reviews on this topic
(see e.g.: Labanowski & Andzelm, 1991; Parr & Yang, 1989; Seminario & Politzer 1995; Ziegler, 1991; Bartolotti and Flurchick, 1996; St-Amant. 1996).
The G1 database of Pople and coworkers is a benchmark for accuracy of the traditional ab initio methods.
The database containes 55 molecules for which experimental values of atomization energies are known within
1 kcal/mol. Curtiss et al (1991) achieved the 1.2 kcal/mol mean absolute error for these 55 atomization
energies using the G2 procedure, which is a quite involved prescription incorporating higher order correlated methods.
Becke (1992) was able to reproduce values in this database with a mean absolute error of 3.7 kcal/mol using his NUMOL
program with
gradient corrected functionals. This result was additionally improved by Becke (1993) to 2.4 kcal/mol when portion of
the electron exchange entering the echange-correlation energy, 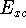 was calculated exactly form Kohn-Sham orbitals
While the error in DFT is considered still too big, these results were obtained with a method
which is substantially less computationally demanding than
original correlated ab initio procedures used by Pople and coworkers. Obviusly, the errors refer to absolute
atomization energies, which in general are very difficult to calculate with good occuracy
(for review see, e.g., Hehre et al, 1986). The relative differences are usually reproduced much better
with DFT methods.
was calculated exactly form Kohn-Sham orbitals
While the error in DFT is considered still too big, these results were obtained with a method
which is substantially less computationally demanding than
original correlated ab initio procedures used by Pople and coworkers. Obviusly, the errors refer to absolute
atomization energies, which in general are very difficult to calculate with good occuracy
(for review see, e.g., Hehre et al, 1986). The relative differences are usually reproduced much better
with DFT methods.
Even without gradient corrections DFT results for bond dissociation energies
are usually much better then the Hartree-Fock (which routinely underbinds) results,
though they have an overbinding tendency. The LDA results are approximately of MP2
quality. The inclusion of gradient corrections to DFT provides bond dissociaction
energies which pair in occuracy with MP4 and CC results.
Molecular geometries even with LSD are much better than corresponding HF results
and are of the MP2 quality. However, LSD fails to correctly treat hydrogen
bonding. This deficiency is removed when one uses gradient corrected DFT approaches.
Quite estonishingly, DFT provides excellent results for molecules which
are notoriously difficult for traditional ab initio approaches
like FOOF, FON, and metalorganic or inorganic moities. There seems to be a funny
regularity: "If something does not work with ab initio, try it with
DFT, and vice versa".
Transition states of organic molecules are frequently not reproduced
well with "pure" DFT. However, it seems that admixture of exact
exchange (see Becke, 1993) via ACM dramatically improves
the problem cases. DFT is however a metod of
choice for transition states in metalorganic reactions.
These systems are notoriously difficult to treat with even
high quality ab initio and have problems with convergence.
Vibrational frequencies are well reproduced even by LSD, though
gradient corrections improve agreement with experiment even
further.
Ionization potentials, electron affinities, and proton
affinities are reproduced fairly well within
gradient corrected DFT.
Recently, there is much interest in using DFT for
high spin species, since preliminary results
are very promissing. On the other hand good
performance of DFT in this field comes as a surprise,
since high multiplets are poorly described by
a single determinant wave function. For all the wrong reasons,
with KS wave function of broken symmetry, the multiplets
splitting are quite well reproduced by DFT.
The scope of applcations for DFT grows rapidly
with calculations of new molecular properties being
added to actively developed software. Recent extensions
include parameters for NMR and ESR spectroscopy,
diamagnetic properties, polarizabilities, relativistic
calculations, and others.
The DFT methodology is still far from mature. It is encouraging
that several groups which were primarily focused on the
development of traditional ab initio approaches
are now actively working in the DFT area. It will bring
new methodological developments, as well as, more
carefull assesment of applicability.
With all the hopes which DFT brings, one has to keep
in mind, that it is primarily a ground state oriented
method, and cannot compete with semiempirical and
correlated ab initio methods in calculations concerning
excited states.
Return to index
Next Section
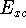 was calculated exactly form Kohn-Sham orbitals
While the error in DFT is considered still too big, these results were obtained with a method
which is substantially less computationally demanding than
original correlated ab initio procedures used by Pople and coworkers. Obviusly, the errors refer to absolute
atomization energies, which in general are very difficult to calculate with good occuracy
(for review see, e.g., Hehre et al, 1986). The relative differences are usually reproduced much better
with DFT methods.
was calculated exactly form Kohn-Sham orbitals
While the error in DFT is considered still too big, these results were obtained with a method
which is substantially less computationally demanding than
original correlated ab initio procedures used by Pople and coworkers. Obviusly, the errors refer to absolute
atomization energies, which in general are very difficult to calculate with good occuracy
(for review see, e.g., Hehre et al, 1986). The relative differences are usually reproduced much better
with DFT methods.